SECCON CTF 14 Quals

Reversing
#

Crown Flash
#

Context & initial static pivot
#

I’m trying to get more familiar with Binary Ninja so I used it for this challenge. The quickest anchor is the user-facing prompt string, so I searched for “Flag:” and followed its code references: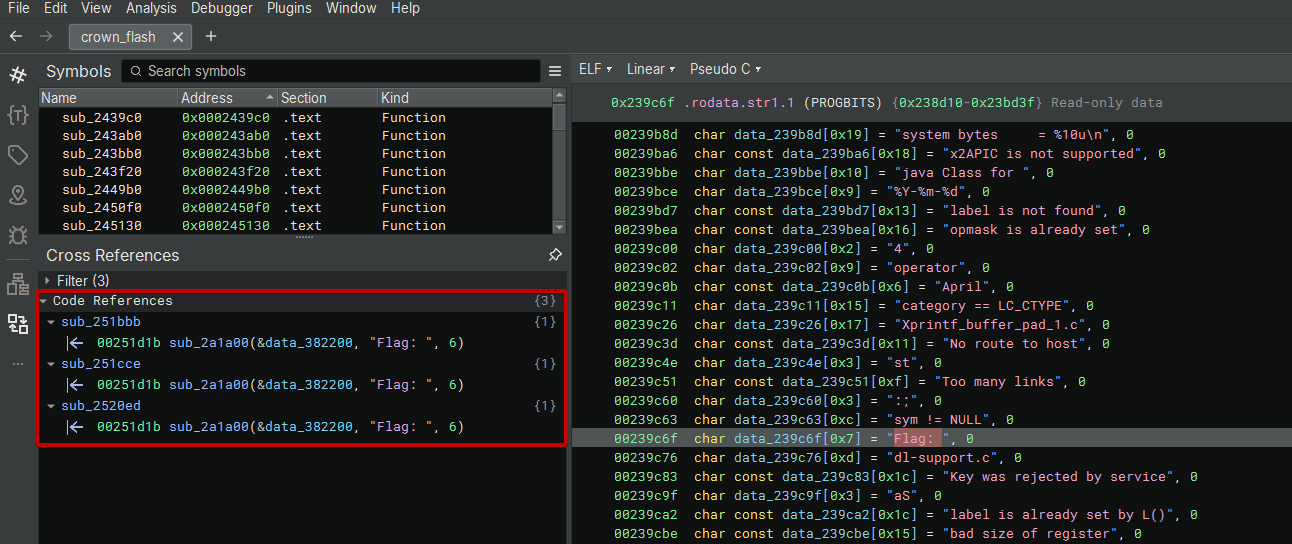

One of the references leads to the main interaction routine:

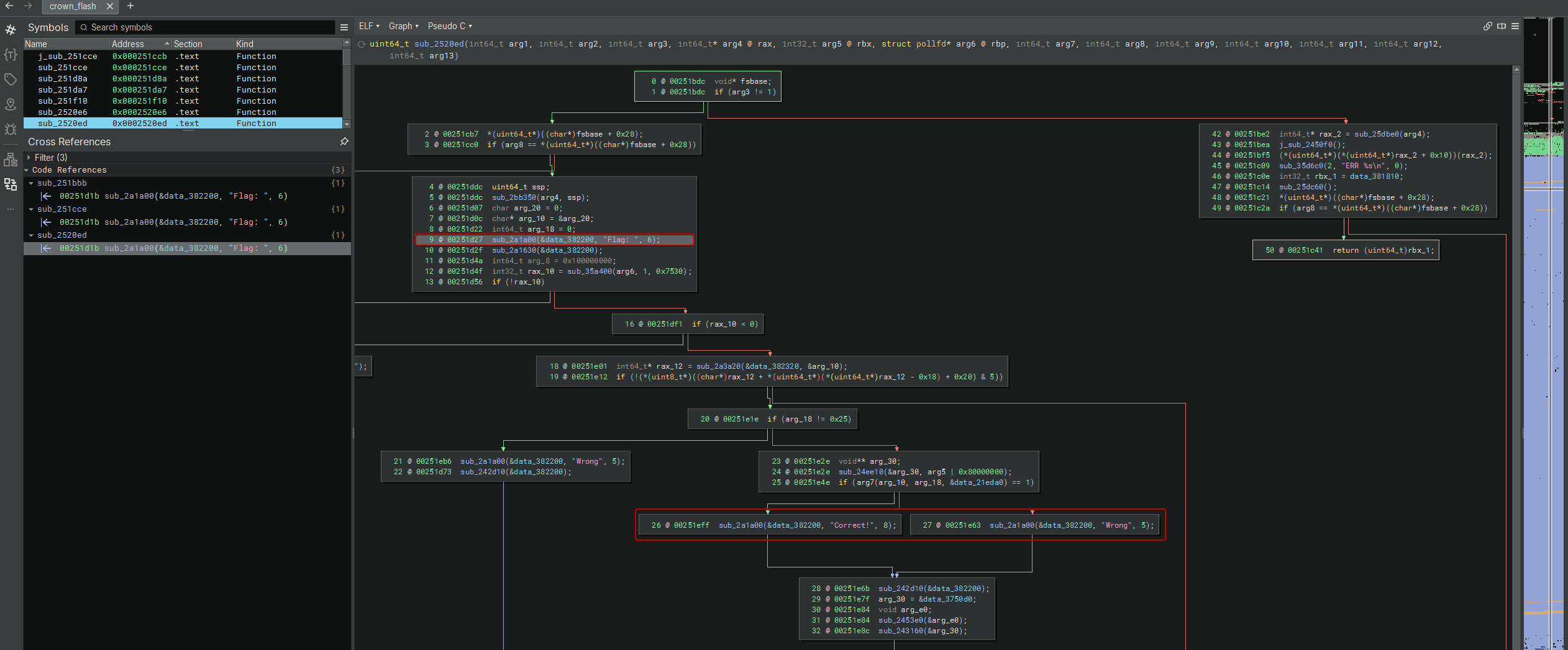
At a high level, this routine:

prints Flag:
waits for input (with a timeout)
reads a line into a buffer
enforces an exact length check (0x25 bytes)
calls a validator through an indirect function pointer (critical pivot)
prints Correct! or Wrong

The binary asks for an input (“Flag: …”) and returns Wrong if validation fails. The interesting part is: the validation logic is not fully present in the main .text in an easy-to-follow way. Instead, it eventually does an indirect call into a memory area that looks like:

not part of the main ELF’s .text
not part of libc
typically a anonymous executable mapping (often RWX in CTF packers/JIT-style stubs)

This is a common CTF anti-static pattern: hide the real validator until runtime, then jump to it.

Goal: recover the validator and its associated constants, then rebuild a solver.

Dissecting the “routine” wrapper
#

Binary Ninja shows the routine as sub_251cce(...) with a lot of “mysterious” arguments because it’s inside a larger C++ program and BN is reconstructing a non-trivial calling context. The portion that matters for reversing is the I/O + dispatch logic:

Stack canary / SSP noise (ignore, but recognize it) We see patterns like:

reads from fsbase + 0x28
compares at function exit
calls a noreturn abort-like function on mismatch (sub_35da60)

That’s the standard x86_64 stack protector canary. It’s not part of the challenge logic, but it is useful to recognize so we don’t spend time on it.

Prompt + timeout: poll(..., 0x7530) The routine prints Flag: and then calls:

sub_35a400(arg4, 1, 0x7530) 0x7530 = 30000 ms (30 seconds).

Then:

if return == 0 -> prints Too slow!
if return < 0 -> errors out (poll)
else -> proceeds to read input

This is a typical anti-bruteforce/anti-automation measure, but more importantly it tells that the binary is checking stdin readiness via poll() rather than just blocking on read(). That’s why “syscall-first” debugging is effective:

Input is read through C++ iostream (why the decompile looks “weird”) The visible routine does not directly read(0, buf, ...) in a clean way. It goes through libstdc++ iostreams, then later materializes exactly what the validator needs: a (ptr, len) pair.

That’s why the decompiler shows pointer arithmetic such as: *(rax + *(*rax - 0x18) + 0x20)

This pattern is typical of optimized C++ object layout:

rax is an iostream-related object (think std::istream / std::basic_ios internals),
the *(*rax - 0x18)-style term behaves like a runtime offset used to reach a base-subobject/state area (common with virtual inheritance + Itanium C++ ABI),
the final + 0x20 lands on a field that behaves like a stream state bitmask.

Semantically, the code is checking whether input succeeded using an iostate mask:

badbit = 0x1, eofbit = 0x2, failbit = 0x4 (libstdc++-style layout)
testing & 0x5 means “reject if badbit or failbit is set”
only if the masked result is zero does the routine proceed to validation.

Practical takeaway: we don’t need to fully reverse iostream internals. The register snapshot at the call site proves the actual validator ABI: rdi = input_ptr, rsi = length, rdx = constants_table.

The exact length gate: arg_18 != 0x25

After the stream-state check, the routine enforces:

if (arg_18 != 0x25) -> "Wrong"

This is the first hard constraint we can reliably infer: the flag length is exactly 37 bytes.

A practical implication: when we later reconstruct the validator, our solver should iterate exactly 37 steps and treat the candidate as raw bytes (not necessarily null-terminated).

For now, I’ll create a in.bin with 37 A (without \n):

The real pivot: the validator is an indirect call

Once length matches, the routine does:

sub_24ee10(&arg_30, arg3) (setup / context)
if (arg6(arg_10, arg_18, &data_21eda0) == 1) -> "Correct!" else "Wrong"

This line is the whole challenge:

ok = validator(input_ptr, input_len, table_ptr);

where:

input_ptr is arg_10
input_len is arg_18 (must be 0x25)
table_ptr is &data_21eda0 (the constant table used per index)
validator is arg6, not a fixed symbol, but a function pointer resolved at runtime

This matches our earlier observation of an indirect call *... and establishes the validator signature without needing to fully understand every C++ wrapper call

Finding input capture
#

To find where the candidate flag is read we start by catching read and inspecting registers using the Linux x86_64 ABI:

For read(fd, buf, count):

rdi = fd
rsi = buf
rdx = count

At the catchpoint:

inspect rsi to see what was read (x/s $rsi or x/32bx $rsi)
inspect rdx to see the maximum expected size
use bt to locate where the program continues after the read

This establishes:

the input buffer address
the expected length (or at least the read limit)
the control-flow path into validation

Identifying the pivot
#

Following the backtrace into the main code reveals a key sequence that looks like:

mov    ... , %rdi      ; input pointer
mov    ... , %rsi      ; length
lea    ... , %rdx      ; pointer to a constant table
call   *0xc8(%rsp)     ; indirect call through stack-stored pointer

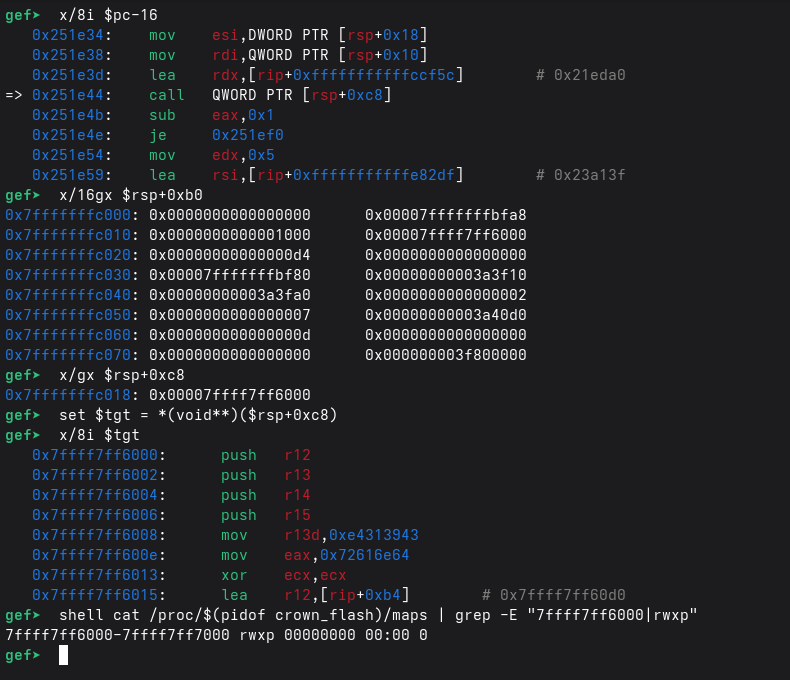
At the call site, the program performs call QWORD PTR [rsp+0xc8], i.e., the validator entrypoint is not a static symbol but a pointer stored on the stack. Dumping that slot (x/gx $rsp+0xc8) reveals the concrete jump target 0x7ffff7ff6000.

Sanity check: the indirect call target (*(void**)($rsp+0xc8)) falls inside the rwxp anonymous mapping, so we’re not guessing, we’re literally jumping into runtime-generated code.

Disassembling that address (x/8i $tgt) shows valid function prologue instructions (pushes and constant initialization), confirming it is executable code. Finally, /proc/<pid>/maps shows 0x7ffff7ff6000-0x7ffff7ff7000 rwxp … 00:00 0, meaning an anonymous RWX page (not backed by the ELF or libc), which is a strong indicator of runtime-generated/unpacked code.

RWX / unpacking / threat model (sanity + implications)

Seeing an anonymous RWX mapping (rwxp + file 00:00 0) is not “normal program behavior” on modern Linux:

Why RWX matters: it means the page is both writable and executable, so the process can generate or decrypt code at runtime and immediately run it. This is a classic pattern for unpacking / JIT / staged validators.
Threat model intuition: the binary is deliberately structured so that the “real logic” is absent from .text and only exists in memory, defeating purely static reversing (strings, xrefs, naive decompile).
Reverse-engineering consequence: the workflow shifts from “find a function in the ELF” to:
1. capture the function pointer (here: the indirect call *0xc8(%rsp) target),
2. confirm the page is executable (info proc mappings / /proc/<pid>/maps),
3. dump the page (dump memory / dump binary memory) and analyze the generated code directly.
Security aside: systems enforcing strict W^X policies typically avoid RWX; CTF binaries often keep it RWX for simplicity, but the concept is the same as real-world loaders (write -> mprotect RX -> execute).

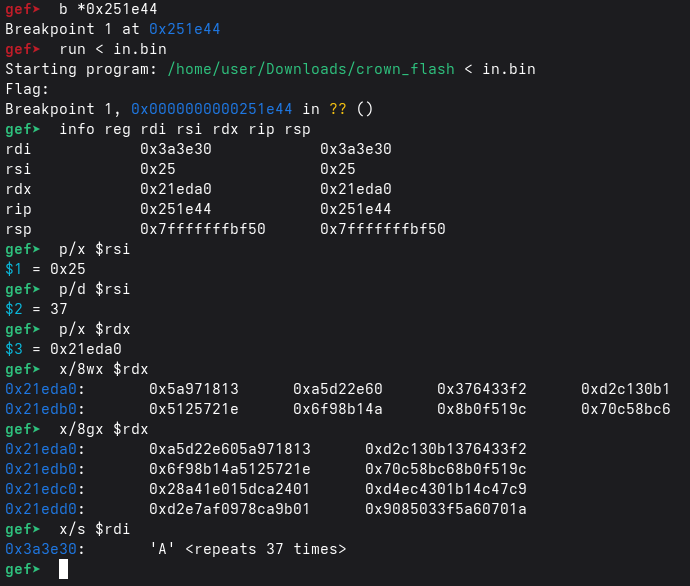
Important observations:

Indirect call (call *0xc8(%rsp))
This is the hallmark: the target is not a fixed symbol, it’s a pointer computed/loaded at runtime.
Registers line up with a classic validator signature:
rdi points at the input string/buffer
rsi is the input length (here: 37, 0x25)
rdx points at a table of constants used during validation

Into runtime code
#

a.k.a the hidden validator

Single-stepping (si) over the call *... moves RIP into an address like:
0x00007ffff7ff6000 (cf. gef screenshot above)

That address range is suspicious:

not inside the main binary mapping
not a typical libc .text region
looks like a dedicated mapped page

This strongly suggests: the validator code is unpacked/constructed at runtime and executed directly.

The fastest way forward is to dump the page and analyze it.

Dumping runtime artifacts
#

We dump the validator page which is a typical size of 0x1000 bytes:

dump binary memory validator.bin 0x7ffff7ff6000 0x7ffff7ff7000

We dump the constant table used by the validator.

The table is addressed via (%rdx, %rcx, 4) = that’s an array of 32-bit words.
Length is 37 = 37 dwords = 148 bytes = 0x94

If table base is 0x21eda0, then end is:

0x21eda0 + 0x94 = 0x21ee34

dump binary memory table.bin 0x21eda0 0x21ee34

We dump the 4-byte cycling XOR key (the “salt”)

Near the end of the validator, a short 4-byte region is used via (i & 3) indexing:

x/4bx 0x7ffff7ff60d0

Observed bytes:

42 19 66 99

Reading the validator logic
#

The validator iterates over each byte of the input and maintains a 32-bit accumulator/state (eax).

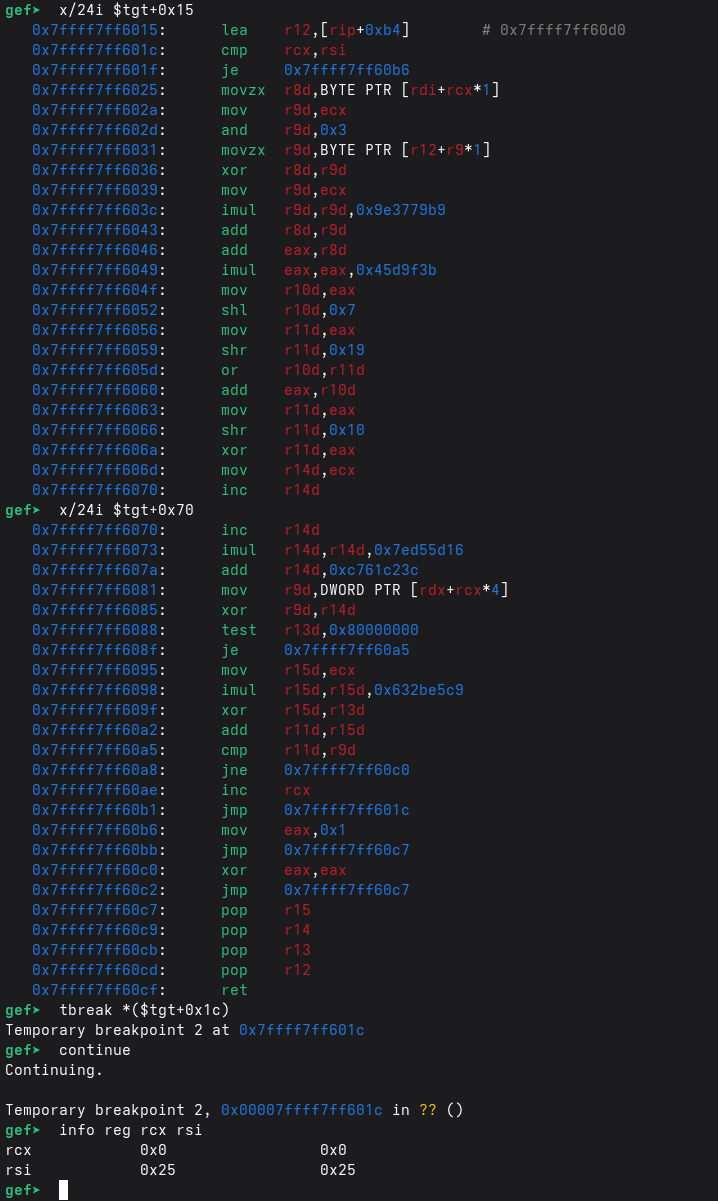
The loop structure is explicit in the dumped validator page:

cmp rcx, rsi; je ... shows rsi is the loop bound (input length) and rcx is the byte index.
movzx r8d, BYTE PTR [rdi+rcx] confirms rdi is the input buffer.
mov r9d, DWORD PTR [rdx+rcx*4] confirms rdx is the base of a uint32_t table indexed by i (rcx), matching the (%rdx,%rcx,4) addressing used to justify dumping 37 dwords.
and r9d, 0x3 + movzx r9d, BYTE PTR [r12+r9] shows the 4-byte XOR key is selected via (i & 3) from a small byte array at r12 (loaded by lea r12, [rip+0xb4]).

For each position i:

Mix the input byte with a 4-byte repeating XOR key
Add an index-dependent constant (i * 0x9E3779B9)
Fold it into eax with multiply/rotate-style avalanche
Derive a check value (r11) from eax
Mix a per-index constant (r14) with a table entry
Compare computed vs expected; fail fast on mismatch

This is a classic “rolling hash with per-position targets”.

Why byte-by-byte
#

At step i, the check is F(eax_i, b_i, i, table[i]) == 0, where eax_i is fully determined by bytes [0..i-1]. Therefore we can enumerate b_i ∈ [0..255] independently, then advance state.

So at iteration i, the check depends on:

the previous state eax (which depends on earlier bytes only)
the current candidate byte b
constants (table[i], XOR key, multipliers)

So for each position, brute-forcing b ∈ [0..255] is feasible:

test each byte
keep the one that satisfies the equality
advance to the next index with the updated eax

In many CTF validators, there is exactly one satisfying byte per index, producing a unique solution.

Reconstructed algorithm
#

Constants:

K4 = [0x42, 0x19, 0x66, 0x99]
EAX0 = 0x72616E64
C1 = 0x9E3779B9
C2 = 0x045D9F3B
C3 = 0x7ED55D16
C4 = 0xC761C23C

All arithmetic is modulo 2^32.

For index i and input byte b:

r8 = (b & 0xFF) ^ K4[i & 3]
r8 = r8 + (i * C1)
eax = eax + r8
eax = eax * C2
eax = eax + rol32(eax, 7)
r11 = eax ^ (eax >> 16)
r14 = (i + 1) * C3 + C4
target = table[i] ^ r14
check: r11 == target

If any index fails, the validator returns 0. If all 37 positions pass, it returns 1.

As you could think it depends on r13d but it works so I guess it’s ok.

Python solver
#

#!/usr/bin/env python3
"""
crown_flash (SECCON) - byte-by-byte stateful solver (pretty output)

- Replays the validator's per-byte update of EAX
- Inverts each step by brute-forcing the next input byte (0..255)
- Produces a readable trace suitable for screenshots
"""

from __future__ import annotations

import argparse
import string
import sys
import time
from typing import Tuple

# ---- Constants extracted from GDB ----

KEY = [0x42, 0x19, 0x66, 0x99]  # bytes at 0x7ffff7ff60d0

TABLE = [
    0x5A971813, 0xA5D22E60, 0x376433F2, 0xD2C130B1,
    0x5125721E, 0x6F98B14A, 0x8B0F519C, 0x70C58BC6,
    0x5DCA2401, 0x28A41E01, 0xB14C47C9, 0xD4EC4301,
    0x78CA9B01, 0xD2E7AF09, 0x5A60701A, 0x9085033F,
    0x6C8CF2D3, 0xC7C7F866, 0x308E6A2B, 0xD583D812,
    0x8B797162, 0xB4B76B2B, 0xA68736B6, 0x5E0F2E8D,
    0xA0FF2519, 0x594F9386, 0x52F9812B, 0x5480290B,
    0xD7B19C6A, 0x23B7ABED, 0xEA18BE84, 0xC50EE1A8,
    0xA5E30ABF, 0x3BED05CE, 0x82052868, 0xA3930232,
    0x69F8AB3B,
]

MASK32 = 0xFFFFFFFF

C1 = 0x9E3779B9
C2 = 0x045D9F3B
C3 = 0x7ED55D16
C4 = 0xC761C23C

INIT_EAX = 0x72616E64  # from: mov $0x72616e64,%eax

# ---------------------------------------------------------------------------


def u32(x: int) -> int:
    return x & MASK32


def rol32(x: int, r: int) -> int:
    x = u32(x)
    return u32((x << r) | (x >> (32 - r)))


def step(eax: int, i: int, b: int) -> Tuple[int, int]:
    """
    Mirrors the validator's per-byte update.

    - r8 = (byte ^ KEY[i&3]) + (i * C1)
    - eax = (eax + r8) * C2
    - eax = eax + rol(eax, 7)
    - r11 = (eax >> 16) ^ eax
    """
    r8 = (b ^ KEY[i & 3]) & 0xFF
    r8 = u32(r8 + u32(i * C1))

    eax2 = u32(eax + r8)
    eax2 = u32(eax2 * C2)
    eax2 = u32(eax2 + rol32(eax2, 7))

    r11 = u32((eax2 >> 16) ^ eax2)
    return eax2, r11


# ---- Pretty printing helpers ----

class Style:
    def __init__(self, color: bool) -> None:
        self.color = color and sys.stdout.isatty()

    def _c(self, code: str, s: str) -> str:
        if not self.color:
            return s
        return f"\x1b[{code}m{s}\x1b[0m"

    def bold(self, s: str) -> str:  return self._c("1", s)
    def dim(self, s: str) -> str:   return self._c("2", s)
    def red(self, s: str) -> str:   return self._c("31", s)
    def green(self, s: str) -> str: return self._c("32", s)
    def cyan(self, s: str) -> str:  return self._c("36", s)
    def yellow(self, s: str) -> str:return self._c("33", s)


def printable_byte(b: int) -> str:
    ch = chr(b)
    if ch in string.printable and ch not in "\r\x0b\x0c":
        if ch == "\n":
            return r"\n"
        if ch == "\t":
            return r"\t"
        return ch
    return "."


def progress_bar(i: int, total: int, width: int = 28) -> str:
    done = int(width * (i / total))
    return "[" + "#" * done + "-" * (width - done) + "]"


def solve(verbose: bool, color: bool, delay: float) -> bytes:
    st = Style(color)

    eax = INIT_EAX
    out = bytearray()
    n = len(TABLE)

    if verbose:
        print(st.bold("crown_flash solver"))
        print(st.dim(f"- bytes: {n}"))
        print(st.dim(f"- init eax: 0x{INIT_EAX:08x}"))
        print(st.dim(f"- key: {', '.join(f'0x{x:02x}' for x in KEY)}"))
        print(st.dim("- note: r15-branch intentionally NOT applied"))
        print()

    t0 = time.time()

    for i in range(n):
        # target = table[i] ^ (((i+1)*C3) + C4)
        r14 = u32(u32((i + 1) * C3) + C4)
        target = u32(TABLE[i] ^ r14)

        found = None
        next_eax = None

        for b in range(256):
            eax2, r11 = step(eax, i, b)
            if r11 == target:
                found = b
                next_eax = eax2
                break

        if found is None or next_eax is None:
            raise RuntimeError(f"No byte found at index {i} (eax=0x{eax:08x})")

        out.append(found)

        if verbose:
            bar = progress_bar(i + 1, n)
            ch = printable_byte(found)
            partial = out.decode("ascii", errors="replace")
            print(
                f"{st.cyan(bar)} {st.bold(f'{i:02d}/{n-1:02d}')}  "
                f"eax={st.yellow(f'0x{eax:08x}')}  "
                f"target={st.dim(f'0x{target:08x}')}  "
                f"byte={st.green(f'0x{found:02x}')}('{st.green(ch)}')  "
                f"-> eax'={st.yellow(f'0x{next_eax:08x}')}  "
                f"{st.dim('partial=')}\"{partial}\""
            )
            if delay > 0:
                time.sleep(delay)

        eax = next_eax

    dt = time.time() - t0
    result = bytes(out)

    if verbose:
        print()
        print(st.bold("Result"))
        try:
            s = result.decode("ascii")
            print(st.green(s))
        except UnicodeDecodeError:
            print(st.green(repr(result)))
        print(st.dim(f"done in {dt:.3f}s"))

    return result


def main() -> None:
    ap = argparse.ArgumentParser(description="crown_flash solver (pretty output)")
    ap.add_argument("-q", "--quiet", action="store_true", help="only print the final flag")
    ap.add_argument("--no-color", action="store_true", help="disable ANSI colors")
    ap.add_argument("--delay", type=float, default=0.0, help="sleep N seconds between steps (for nicer screenshots/videos)")
    args = ap.parse_args()

    flag = solve(verbose=not args.quiet, color=not args.no_color, delay=args.delay)

    if args.quiet:
        try:
            print(flag.decode("ascii"))
        except UnicodeDecodeError:
            print(flag)


if __name__ == "__main__":
    main()

Sanity checks
#

To be confident the reconstruction is correct we:

Confirm the validator reads table[i] as dword:
- instruction pattern: mov (%rdx,%rcx,4), %r9d
Confirm input length is fixed:
- rsi == 0x25 at the validator entry
Confirm the XOR key is used with (i & 3):
- pattern: and $0x3, reg then movzbl (key + reg), ...

What I learnt
#

Syscall-first dynamic reversing is the fastest route when symbols are stripped and code is relocated.
An indirect call into a “weird” region is a strong unpack/JIT indicator.
Dumping a runtime validator + constants is often all that’s needed to solve.
Rolling-state validators are frequently solvable incrementally (256 brute-force per byte) when each index has an independent target.

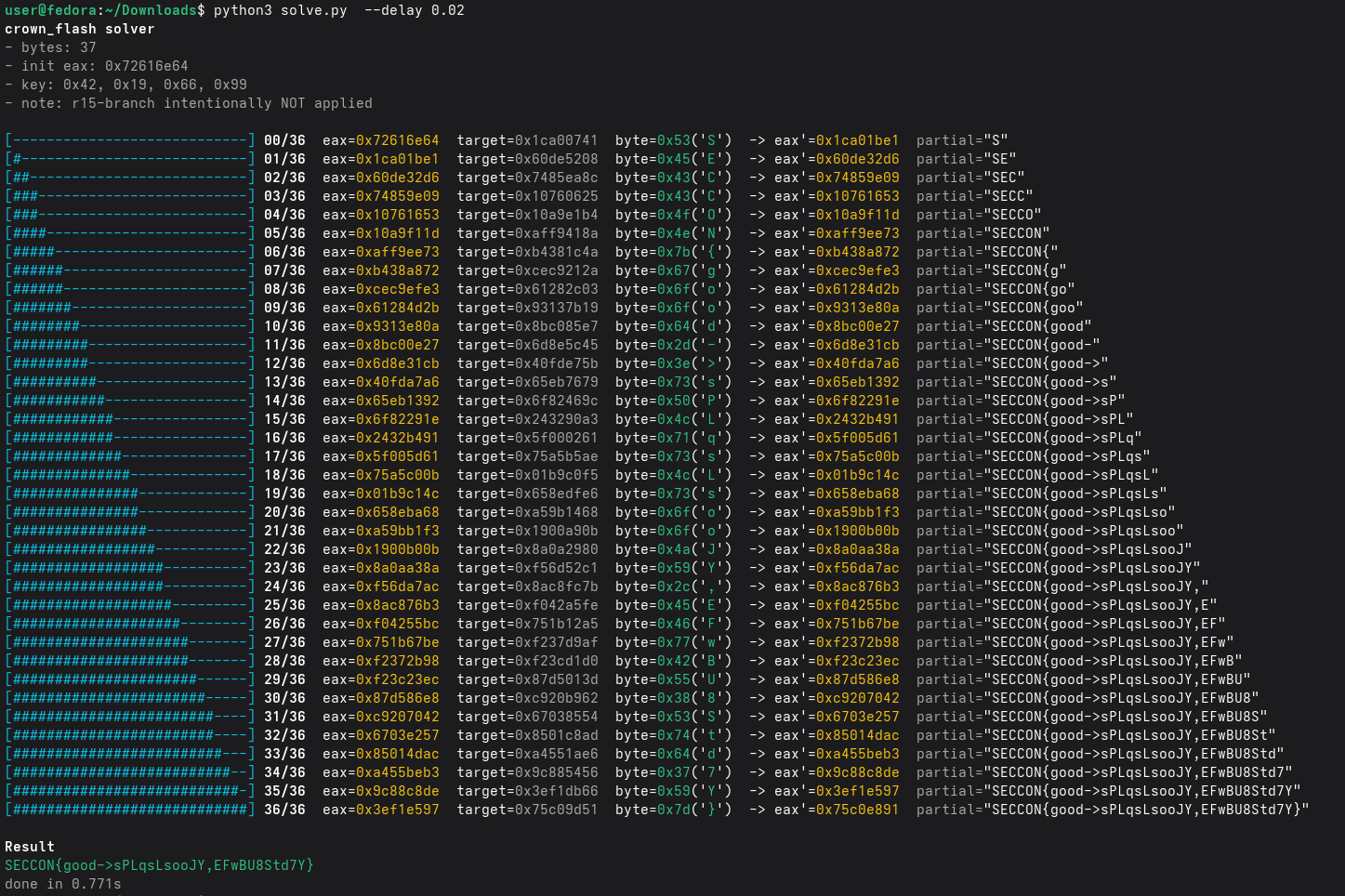
FLAG: SECCON{good->sPLqsLsooJY,EFwBU8Std7Y}

Reversing#

Crown Flash#

Context & initial static pivot#

Dissecting the “routine” wrapper#

Finding input capture#

Identifying the pivot#

Into runtime code#

Dumping runtime artifacts#

Reading the validator logic#

Why byte-by-byte#

Reconstructed algorithm#

Python solver#

Sanity checks#

What I learnt#