SECCON CTF 14 予選

⚠️ この文章は ChatGPT で作成しました（日本語はまだ N4 レベルです）。

リバース
#

Crown Flash
#

コンテキストと最初の静的な足がかり
#

Binary Ninja にもっと慣れたかったので、この問題は BN を使って進めた。まず最速で刺さるアンカーは、ユーザー向けに出てくるプロンプト文字列。なので “Flag:” を文字列検索して、そこへの code reference を追った: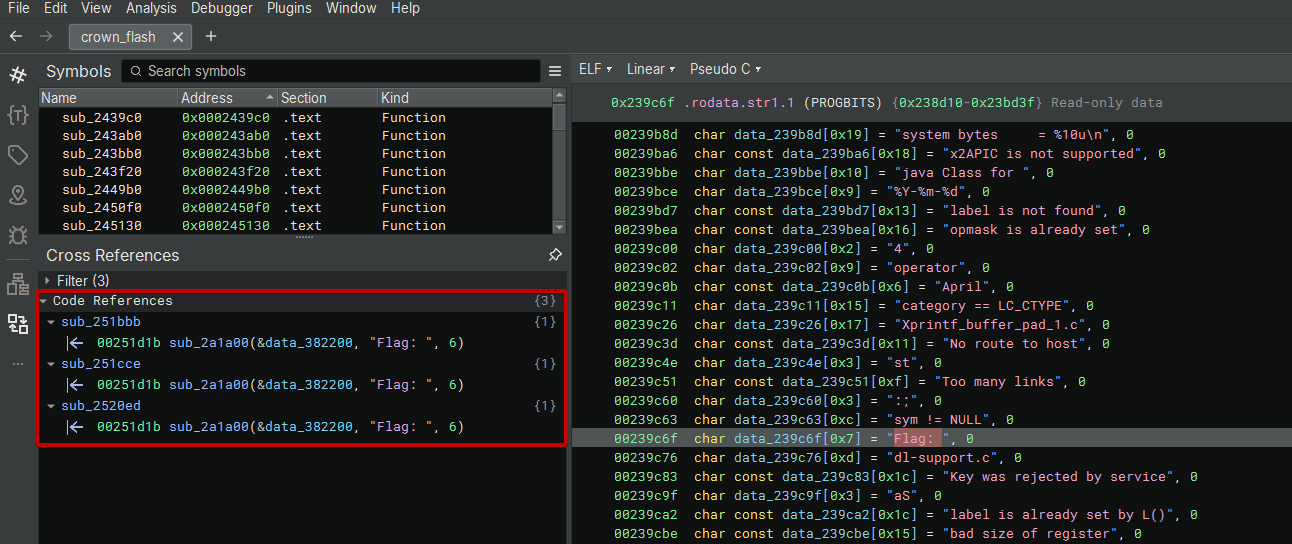

参照のひとつが、メインの対話ルーチンに繋がっている:

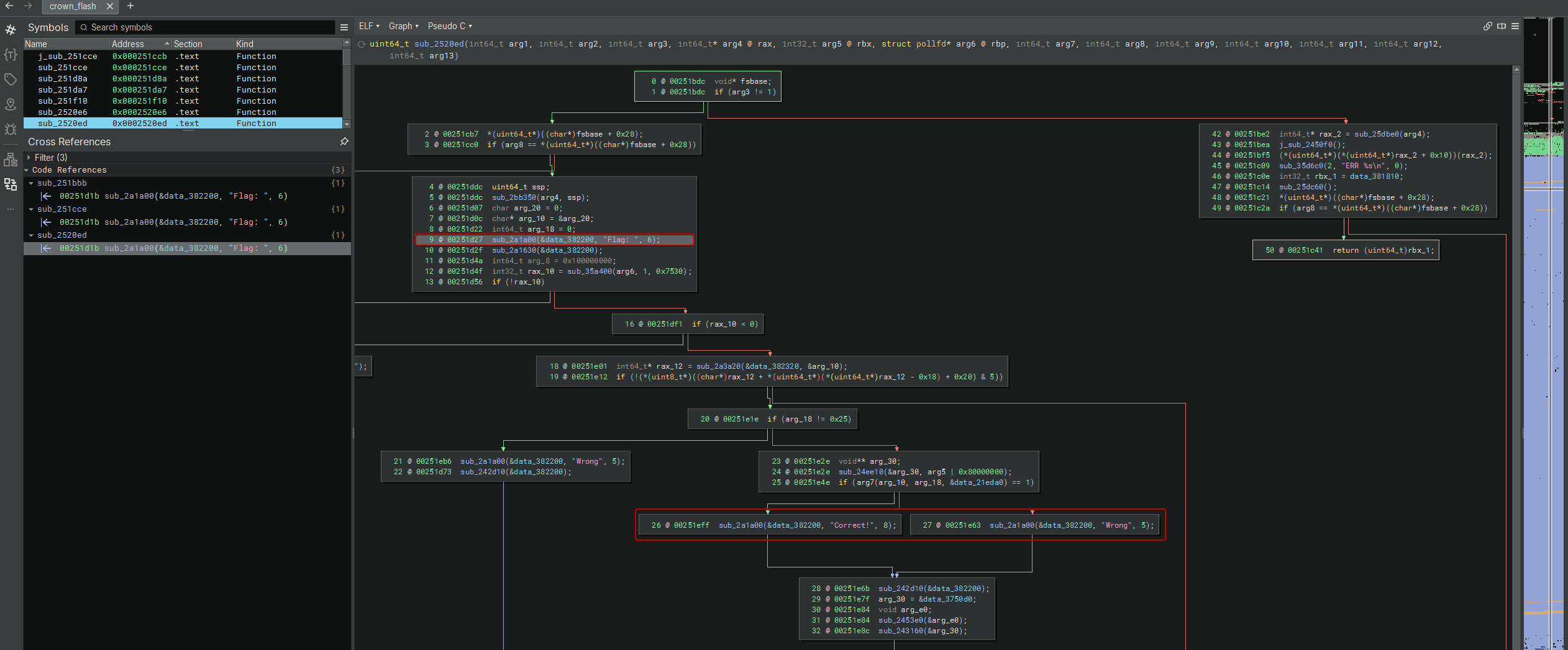
ざっくり言うと、このルーチンは:

Flag: を表示
入力待ち（タイムアウト付き）
1 行をバッファに読み込み
長さがちょうど 0x25 バイトかを強制チェック
間接関数ポインタ 経由でバリデータを呼ぶ（ここが重要なピボット）
Correct! か Wrong を表示

バイナリは入力 (“Flag: …”) を要求し、検証に失敗すると Wrong を返す。面白いのは、検証ロジックがメインの .text に「素直に読める形」で全部は載っていないこと。代わりに最終的に、次のようなメモリ領域への 間接 call になっている:

メイン ELF の .text ではない
libc の一部でもない
典型的には 匿名の実行可能マッピング（CTF のパッカー／JIT っぽいスタブでよくある RWX）

これは CTF でよくあるアンチ静的解析のパターン: 本物のバリデータを実行時まで隠し、展開してからそこへジャンプする。

ゴール: バリデータ本体とそれに紐づく定数を回収し、ソルバを組み直す。

「routine」ラッパーの分解
#

Binary Ninja はこのルーチンを sub_251cce(...) として表示していて、C++ の大きめプログラムの中にあるせいで引数が「謎」っぽく見える（BN が非自明な呼び出しコンテキストを復元している）。ただ、リバースで本当に必要なのは I/O とディスパッチ部分なので、そこだけ押さえる。

スタックカナリア / SSP のノイズ（無視していいが、見分けられるようにする） 次のようなパターンが見える:

fsbase + 0x28 から読み出す
関数終了時に比較する
不一致なら noreturn の abort っぽい関数を呼ぶ（sub_35da60）

これは x86_64 のスタックプロテクタ（カナリア）の定番。チャレンジロジックではないので深追い不要だけど、認識できると時間を溶かさずに済む。

プロンプト + タイムアウト: poll(..., 0x7530) ルーチンは Flag: を出してから、

sub_35a400(arg4, 1, 0x7530) を呼ぶ。0x7530 = 30000 ms（30 秒）。

その後:

戻り値が 0 -> Too slow!
戻り値が 0 未満 -> エラー終了（poll）
それ以外 -> 入力を読む

典型的なアンチ総当たり／アンチ自動化だけど、それ以上に重要なのは「stdin の準備完了チェックに poll() を使っていて、単純に read() でブロックしていない」点。だから “syscall-first” なデバッグが刺さる:

入力は C++ iostream 経由（デコンパイルが「変」に見える理由） 見えているルーチンは、綺麗に read(0, buf, ...) を叩いているわけじゃなくて、libstdc++ の iostream を通して読んでいる。その後に「バリデータが欲しい形」で (ptr, len) のペアが具体化される。

なのでデコンパイラ上では、例えば *(rax + *(*rax - 0x18) + 0x20) みたいなポインタ演算が出てくる。

この形は最適化された C++ のオブジェクトレイアウトでは割と典型:

rax は iostream 関連のオブジェクト（std::istream / std::basic_ios の内部みたいなもの）
*(*rax - 0x18) っぽい項は、実行時オフセットでベースのサブオブジェクト／状態領域へ到達するためのもの（仮想継承 + Itanium C++ ABI でよくある）
最後の + 0x20 は、ストリーム状態ビットマスクっぽいフィールドに着地する

意味としては、iostate マスクで「入力が成功したか」を判定している:

badbit = 0x1, eofbit = 0x2, failbit = 0x4（libstdc++ っぽい）
& 0x5 のテストは「badbit か failbit が立ってたら拒否」
その結果が 0 のときだけ検証に進む

実務上の結論: iostream の内部を全部リバースする必要はない。呼び出し地点のレジスタスナップショットを見れば、バリデータの ABI は確定できる: rdi = input_ptr, rsi = length, rdx = constants_table.

長さがピッタリのゲート: arg_18 != 0x25

ストリーム状態チェックの後に、このルーチンは

if (arg_18 != 0x25) -> "Wrong" を強制する。

ここから確実に言える最初のハード制約は、フラグ長が ちょうど 37 バイト ということ。

実務的な含意: 後でバリデータを再構築するとき、ソルバは必ず 37 ステップを回し、候補は raw bytes として扱う（ヌル終端前提ではない）。

ひとまず \n なしで 37 個の A を入れた in.bin を作る:

本当のピボット: バリデータは間接 call

長さが一致すると、ルーチンは:

sub_24ee10(&arg_30, arg3)（セットアップ／コンテキスト）
if (arg6(arg_10, arg_18, &data_21eda0) == 1) -> "Correct!" else "Wrong" を実行する。

この 1 行がチャレンジの中核:

ok = validator(input_ptr, input_len, table_ptr);

ここで:

input_ptr は arg_10
input_len は arg_18（0x25 必須）
table_ptr は &data_21eda0（インデックスごとに使う定数テーブル）
validator は固定シンボルではなく arg6（実行時に解決される関数ポインタ）

これは先に見た「間接 call *...」の観察と一致し、C++ のラッパー周りを全部理解しなくてもバリデータのシグネチャが固まる。

入力キャプチャの特定
#

候補フラグがどこで読まれているかを掴むために、まず read を捕まえて Linux x86_64 ABI のレジスタを確認する。

read(fd, buf, count) の呼び出しでは:

rdi = fd
rsi = buf
rdx = count

catchpoint で:

rsi を見て何が読まれたか確認（x/s $rsi や x/32bx $rsi）
rdx を見て最大サイズを確認
bt で read 以降の制御フローを辿る

これで:

入力バッファのアドレス
期待される長さ（または少なくとも read 上限）
検証に入るまでの経路が確定できる。

ピボットの同定
#

バックトレースを追っていくと、次のような並びが見つかる:

mov    ... , %rdi      ; input pointer
mov    ... , %rsi      ; length
lea    ... , %rdx      ; pointer to a constant table
call   *0xc8(%rsp)     ; indirect call through stack-stored pointer

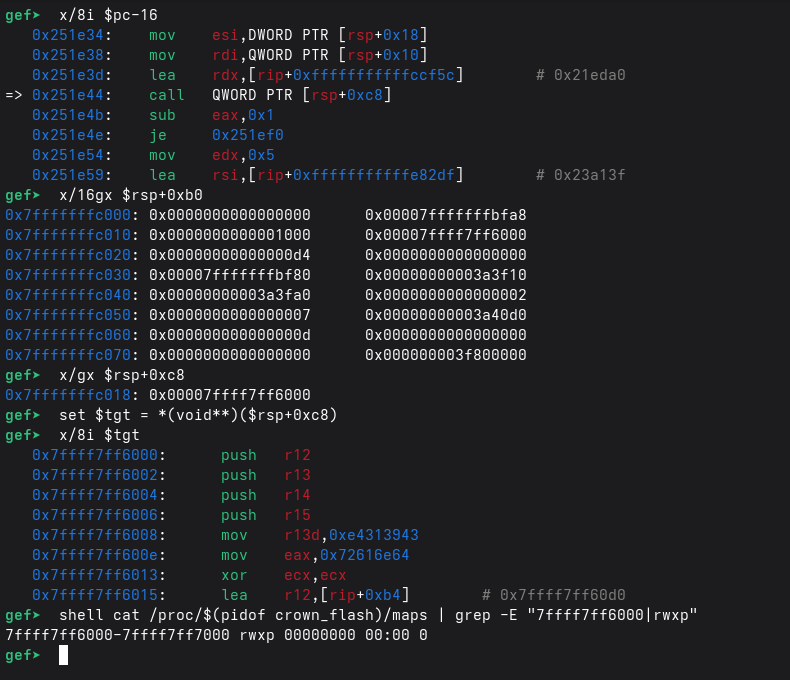
呼び出し地点では call QWORD PTR [rsp+0xc8] になっていて、つまりバリデータのエントリポイントは静的シンボルではなく、スタック上に置かれたポインタ。そこをダンプ（x/gx $rsp+0xc8）すると、具体的なジャンプ先 0x7ffff7ff6000 が出てくる。

サニティチェック: この間接 call のターゲット（*(void**)($rsp+0xc8)）は、rwxp の匿名マッピング内に落ちている。推測ではなく「実際に」実行時生成コードへ飛んでいる。

そのアドレスを逆アセンブル（x/8i $tgt）すると、push などのプロローグと定数初期化が見え、実行可能コードであることが確認できる。さらに /proc/<pid>/maps では 0x7ffff7ff6000-0x7ffff7ff7000 rwxp … 00:00 0 となり、ELF や libc に紐づかない 匿名 RWX ページ（典型的な「実行時に展開される／アンパックされるコード」の強いサイン）だと分かる。

RWX / unpacking / threat model（確認と含意）

匿名 RWX マッピング（rwxp かつファイルが 00:00 0）を見るのは、最近の Linux では「普通のプログラムの挙動」ではない:

RWX が意味するもの: ページが writable かつ executable なので、プロセスは実行時にコードを 生成／復号 して、その場で実行できる。これは unpacking / JIT / 段階的バリデータ の定番パターン。
脅威モデル感: バイナリは意図的に「本体ロジック」を .text から外し、メモリ上にだけ存在させることで、純静的解析（文字列、xrefs、雑なデコンパイル）を潰している。
リバース上の帰結: 以降のワークフローは「ELF 内の関数を探す」から、
1. 間接 call 先の 関数ポインタ を捕まえる（ここでは call *0xc8(%rsp) のターゲット）、
2. ページが 実行可能 であることを確認（info proc mappings / /proc/<pid>/maps）、
3. ページを dump（dump memory / dump binary memory）して、生成コードを直接解析に切り替わる。
セキュリティ余談: 厳格な W^X を強制する環境では RWX は避けることが多い。CTF バイナリは簡便さのため RWX のままにしがちだが、実世界のローダでもコンセプトは同じ（write -> mprotect で RX -> execute）。

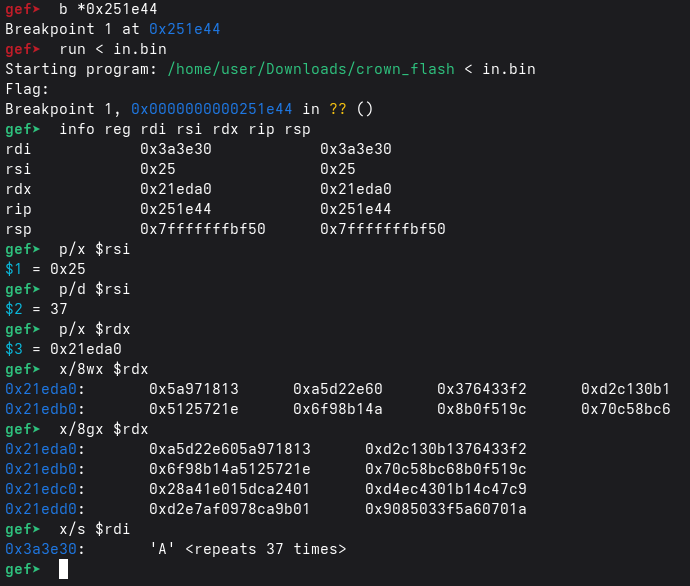
重要な観察:

間接 call（call *0xc8(%rsp)）
これが決定的。ターゲットが固定シンボルではなく、実行時に読み込まれるポインタ。
レジスタが典型的なバリデータ・シグネチャに一致:
rdi が入力文字列／バッファを指す
rsi が入力長（ここでは 37、0x25）
rdx が 定数テーブル を指す（検証中にインデックスごとに使用）

実行時コードへ
#

いわゆる hidden validator

call *... を si で踏むと、RIP が例えば次のようなアドレスへ移動する:
0x00007ffff7ff6000 (上の gef スクショ参照)

このレンジは怪しい:

メインバイナリのマッピング外
libc の .text の典型的な領域でもない
1 ページ分だけ確保された専用っぽい範囲

つまり バリデータコードが実行時にアンパック／構築されて、そのまま実行されている 可能性が高い。

最短ルートは、そのページを dump して解析すること。

実行時アーティファクトのダンプ
#

バリデータページを dump。サイズは典型的に 0x1000 バイト:

dump binary memory validator.bin 0x7ffff7ff6000 0x7ffff7ff7000

バリデータが使う定数テーブルも dump。

テーブルは (%rdx, %rcx, 4) で参照されている = 32-bit word（dword）の配列。
長さは 37 = 37 dwords = 148 bytes = 0x94

ベースが 0x21eda0 なら、終端は:

0x21eda0 + 0x94 = 0x21ee34

dump binary memory table.bin 0x21eda0 0x21ee34

4 バイト周期の XOR キー（“salt”）も dump

バリデータの終盤あたりで、(i & 3) のインデクシングで使われる短い 4-byte 領域がある:

x/4bx 0x7ffff7ff60d0

観測できたバイト列:

42 19 66 99

バリデータロジックの読み取り
#

バリデータは入力の各バイトを舐めつつ、32-bit のアキュムレータ／状態（eax）を維持する。

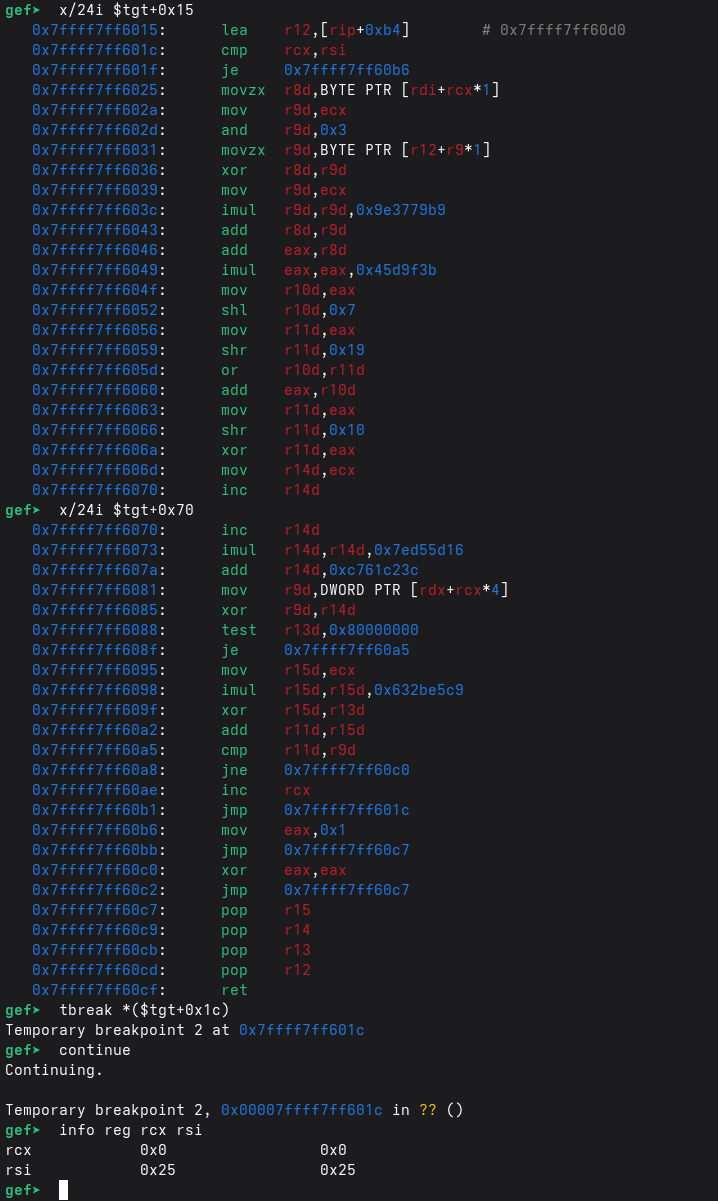
dump したバリデータページから、ループ構造がはっきり見える:

cmp rcx, rsi; je ... で rsi がループ上限（入力長）、rcx がバイトインデックスだと分かる
movzx r8d, BYTE PTR [rdi+rcx] で rdi が入力バッファ
mov r9d, DWORD PTR [rdx+rcx*4] で rdx が uint32_t テーブルのベース、i（rcx）でインデックスされることが分かる（(%rdx,%rcx,4) の根拠そのまま）
and r9d, 0x3 + movzx r9d, BYTE PTR [r12+r9] で、4-byte XOR キーが (i & 3) によって r12 上の小さな配列から選ばれる（lea r12, [rip+0xb4] でロード）

各位置 i ごとに:

入力バイトを 4-byte 周期 XOR キーで混ぜる
インデックス依存の定数（i * 0x9E3779B9）を足す
multiply/rotate 系のアバランチで eax に畳み込む
eax からチェック値（r11）を導く
インデックス依存の定数（r14）をテーブル要素と混ぜる
計算値と期待値を比較し、違えば即失敗

典型的な「ローリングハッシュ + 位置ごとのターゲット」タイプ。

なぜ 1 バイトずつ解けるか
#

ステップ i におけるチェックは F(eax_i, b_i, i, table[i]) == 0 の形で、eax_i はバイト [0..i-1] だけで完全に決まる。なので b_i ∈ [0..255] を独立に総当たりして良い。

つまり反復 i で依存するのは:

直前状態 eax（前のバイトだけで決まる）
今の候補バイト b
定数（table[i]、XOR キー、乗数）

よって各位置ごとに b ∈ [0..255] を試せば十分:

0..255 を試す
等式を満たすものを採用
更新された eax で次のインデックスへ進む

CTF のこの手のバリデータは、多くの場合インデックスごとに成立するバイトが 1 つだけ で、解は一意になる。

再構成したアルゴリズム
#

定数:

K4 = [0x42, 0x19, 0x66, 0x99]
EAX0 = 0x72616E64
C1 = 0x9E3779B9
C2 = 0x045D9F3B
C3 = 0x7ED55D16
C4 = 0xC761C23C

計算はすべて 2^32 での剰余（mod 2^32）。

インデックス i と入力バイト b について:

r8 = (b & 0xFF) ^ K4[i & 3]
r8 = r8 + (i * C1)
eax = eax + r8
eax = eax * C2
eax = eax + rol32(eax, 7)
r11 = eax ^ (eax >> 16)
r14 = (i + 1) * C3 + C4
target = table[i] ^ r14
check: r11 == target

r13d にも依存してそうに見えるけど、動くのでまあヨシ、ということで。

Python ソルバ
#

#!/usr/bin/env python3
"""
crown_flash (SECCON) - byte-by-byte stateful solver (pretty output)

- Replays the validator's per-byte update of EAX
- Inverts each step by brute-forcing the next input byte (0..255)
- Produces a readable trace suitable for screenshots
"""

from __future__ import annotations

import argparse
import string
import sys
import time
from typing import Tuple

# ---- Constants extracted from GDB ----

KEY = [0x42, 0x19, 0x66, 0x99]  # bytes at 0x7ffff7ff60d0

TABLE = [
    0x5A971813, 0xA5D22E60, 0x376433F2, 0xD2C130B1,
    0x5125721E, 0x6F98B14A, 0x8B0F519C, 0x70C58BC6,
    0x5DCA2401, 0x28A41E01, 0xB14C47C9, 0xD4EC4301,
    0x78CA9B01, 0xD2E7AF09, 0x5A60701A, 0x9085033F,
    0x6C8CF2D3, 0xC7C7F866, 0x308E6A2B, 0xD583D812,
    0x8B797162, 0xB4B76B2B, 0xA68736B6, 0x5E0F2E8D,
    0xA0FF2519, 0x594F9386, 0x52F9812B, 0x5480290B,
    0xD7B19C6A, 0x23B7ABED, 0xEA18BE84, 0xC50EE1A8,
    0xA5E30ABF, 0x3BED05CE, 0x82052868, 0xA3930232,
    0x69F8AB3B,
]

MASK32 = 0xFFFFFFFF

C1 = 0x9E3779B9
C2 = 0x045D9F3B
C3 = 0x7ED55D16
C4 = 0xC761C23C

INIT_EAX = 0x72616E64  # from: mov $0x72616e64,%eax

# ---------------------------------------------------------------------------


def u32(x: int) -> int:
    return x & MASK32


def rol32(x: int, r: int) -> int:
    x = u32(x)
    return u32((x << r) | (x >> (32 - r)))


def step(eax: int, i: int, b: int) -> Tuple[int, int]:
    """
    Mirrors the validator's per-byte update.

    - r8 = (byte ^ KEY[i&3]) + (i * C1)
    - eax = (eax + r8) * C2
    - eax = eax + rol(eax, 7)
    - r11 = (eax >> 16) ^ eax
    """
    r8 = (b ^ KEY[i & 3]) & 0xFF
    r8 = u32(r8 + u32(i * C1))

    eax2 = u32(eax + r8)
    eax2 = u32(eax2 * C2)
    eax2 = u32(eax2 + rol32(eax2, 7))

    r11 = u32((eax2 >> 16) ^ eax2)
    return eax2, r11


# ---- Pretty printing helpers ----

class Style:
    def __init__(self, color: bool) -> None:
        self.color = color and sys.stdout.isatty()

    def _c(self, code: str, s: str) -> str:
        if not self.color:
            return s
        return f"\x1b[{code}m{s}\x1b[0m"

    def bold(self, s: str) -> str:  return self._c("1", s)
    def dim(self, s: str) -> str:   return self._c("2", s)
    def red(self, s: str) -> str:   return self._c("31", s)
    def green(self, s: str) -> str: return self._c("32", s)
    def cyan(self, s: str) -> str:  return self._c("36", s)
    def yellow(self, s: str) -> str:return self._c("33", s)


def printable_byte(b: int) -> str:
    ch = chr(b)
    if ch in string.printable and ch not in "\r\x0b\x0c":
        if ch == "\n":
            return r"\n"
        if ch == "\t":
            return r"\t"
        return ch
    return "."


def progress_bar(i: int, total: int, width: int = 28) -> str:
    done = int(width * (i / total))
    return "[" + "#" * done + "-" * (width - done) + "]"


def solve(verbose: bool, color: bool, delay: float) -> bytes:
    st = Style(color)

    eax = INIT_EAX
    out = bytearray()
    n = len(TABLE)

    if verbose:
        print(st.bold("crown_flash solver"))
        print(st.dim(f"- bytes: {n}"))
        print(st.dim(f"- init eax: 0x{INIT_EAX:08x}"))
        print(st.dim(f"- key: {', '.join(f'0x{x:02x}' for x in KEY)}"))
        print(st.dim("- note: r15-branch intentionally NOT applied"))
        print()

    t0 = time.time()

    for i in range(n):
        # target = table[i] ^ (((i+1)*C3) + C4)
        r14 = u32(u32((i + 1) * C3) + C4)
        target = u32(TABLE[i] ^ r14)

        found = None
        next_eax = None

        for b in range(256):
            eax2, r11 = step(eax, i, b)
            if r11 == target:
                found = b
                next_eax = eax2
                break

        if found is None or next_eax is None:
            raise RuntimeError(f"No byte found at index {i} (eax=0x{eax:08x})")

        out.append(found)

        if verbose:
            bar = progress_bar(i + 1, n)
            ch = printable_byte(found)
            partial = out.decode("ascii", errors="replace")
            print(
                f"{st.cyan(bar)} {st.bold(f'{i:02d}/{n-1:02d}')}  "
                f"eax={st.yellow(f'0x{eax:08x}')}  "
                f"target={st.dim(f'0x{target:08x}')}  "
                f"byte={st.green(f'0x{found:02x}')}('{st.green(ch)}')  "
                f"-> eax'={st.yellow(f'0x{next_eax:08x}')}  "
                f"{st.dim('partial=')}\"{partial}\""
            )
            if delay > 0:
                time.sleep(delay)

        eax = next_eax

    dt = time.time() - t0
    result = bytes(out)

    if verbose:
        print()
        print(st.bold("Result"))
        try:
            s = result.decode("ascii")
            print(st.green(s))
        except UnicodeDecodeError:
            print(st.green(repr(result)))
        print(st.dim(f"done in {dt:.3f}s"))

    return result


def main() -> None:
    ap = argparse.ArgumentParser(description="crown_flash solver (pretty output)")
    ap.add_argument("-q", "--quiet", action="store_true", help="only print the final flag")
    ap.add_argument("--no-color", action="store_true", help="disable ANSI colors")
    ap.add_argument("--delay", type=float, default=0.0, help="sleep N seconds between steps (for nicer screenshots/videos)")
    args = ap.parse_args()

    flag = solve(verbose=not args.quiet, color=not args.no_color, delay=args.delay)

    if args.quiet:
        try:
            print(flag.decode("ascii"))
        except UnicodeDecodeError:
            print(flag)


if __name__ == "__main__":
    main()

サニティチェック
#

復元が正しいことを確信するために、次を確認する:

バリデータが table[i] を dword として読む:
- 命令パターン: mov (%rdx,%rcx,4), %r9d
入力長が固定:
- バリデータ入口で rsi == 0x25
XOR キーが (i & 3) で使われる:
- and $0x3, reg の後に movzbl (key + reg), ...

学び
#

シンボルが潰され、コードがリロケートされるタイプは、syscall-first の動的解析が一番早い。
「変な領域」への間接 call は unpack/JIT の強いサイン。
実行時バリデータと定数を dump できれば、それだけで解けることが多い。
ローリング状態のバリデータは、各インデックスでターゲットが独立しているなら 1 バイトずつ（256 総当たり）で解ける。

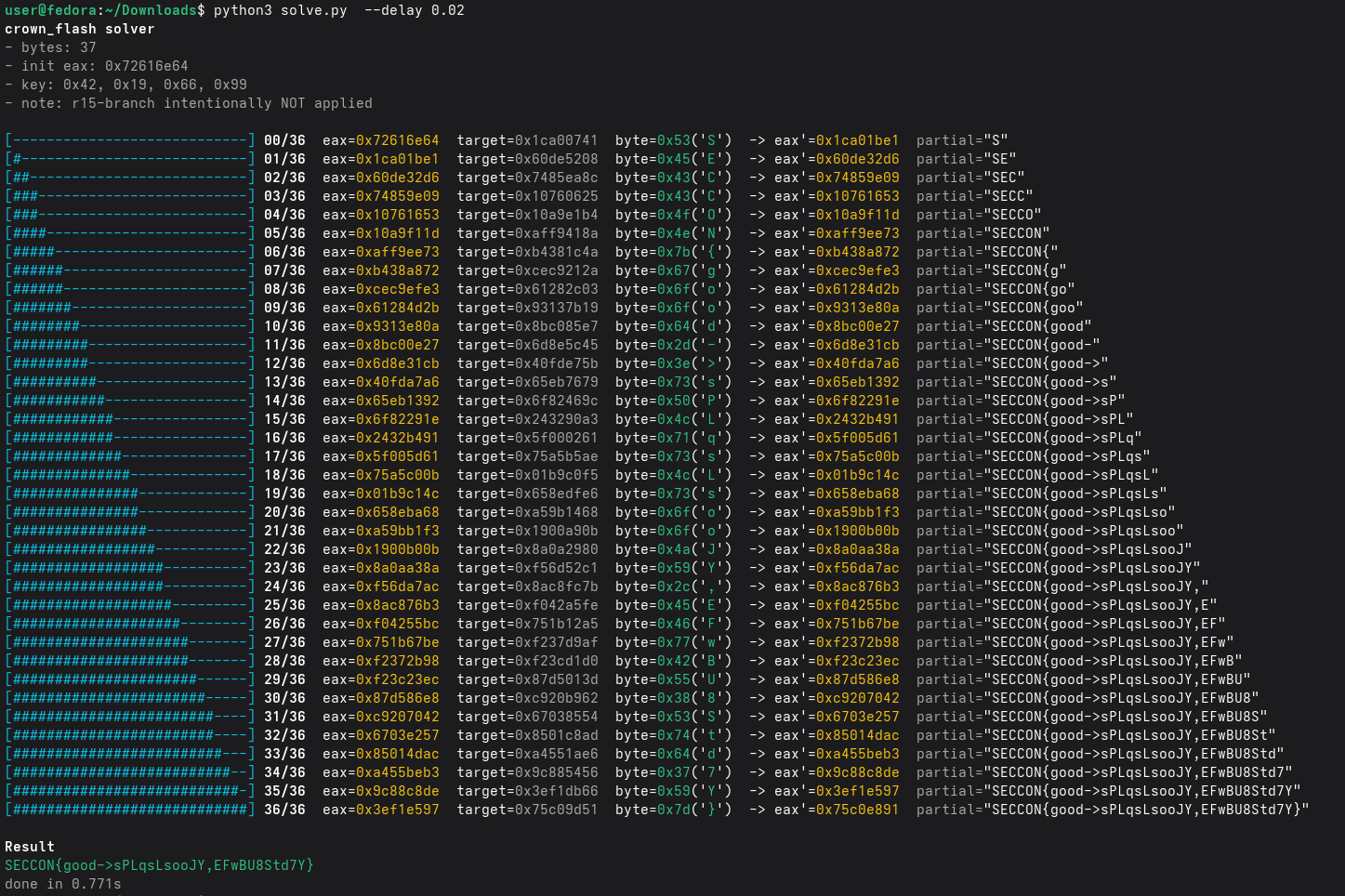
FLAG: SECCON{good->sPLqsLsooJY,EFwBU8Std7Y}

リバース#

Crown Flash#

コンテキストと最初の静的な足がかり#

「routine」ラッパーの分解#

入力キャプチャの特定#

ピボットの同定#

実行時コードへ#

実行時アーティファクトのダンプ#

バリデータロジックの読み取り#

なぜ 1 バイトずつ解けるか#

再構成したアルゴリズム#

Python ソルバ#

サニティチェック#

学び#